
RSA加密算法是现代信息安全的基石,其广泛应用于网络通信、数据加密和电子商务领域。然而,随着量子计算的快速发展,传统密码学面临着前所未有的挑战。特别是在含噪中等规模量子计算(NISQ)时代,基于量子-经典混合方法的VQF(变分量子分解算法)算法,为破解RSA提供了一种全新思路。本文将详细介绍RSA的加密原理,并探索VQF算法如何解密RSA加密的过程及其优势。
01 什么是RSA加密算法?
RSA算法是1977年由RonRivest、AdiShamir和LeonardAdleman提出的公钥加密算法(RSA就是他们三人姓氏开头字母拼在一起组成的)。RSA是目前最有影响力的公钥加密算法,能够抵抗目前为止绝大多数密码攻击,被ISO推荐为公钥数据加密标准。
RSA通过两个密钥(公钥和私钥)来加密和解密数据:
• 公钥:公开的“锁”,任何人都可以用它将信息锁起来(加密)
• 私钥:接收者独有的“钥匙”,只有它才能解开“锁”(解密)
举个例子,小红想给小绿传递情书,但中间有许多传递人,小红不希望内容被他们窥探。小绿提供了一个箱子,上面有一把锁(公钥,此处公钥类比为这把锁),这把锁只能用小绿独有的钥匙(私钥,此处私钥类比为该锁的唯一钥匙)打开。小红拿到箱子后将情书放入并用锁把箱子锁上,然后交给传递人。传递人虽然能拿到箱子和锁(公钥),但没有小绿唯一的钥匙(私钥),因此无法打开箱子。
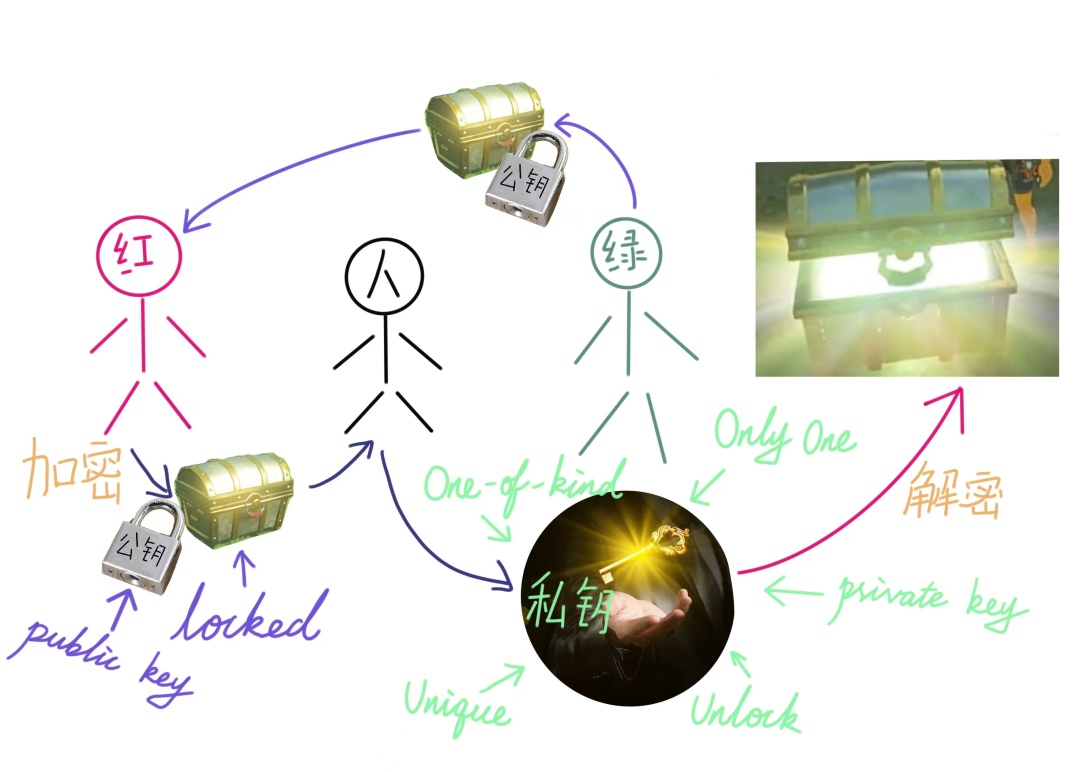
△ 举例
然而,这种加密的安全性依赖于锁的复杂程度,也就是私钥的难以破解性。如果锁足够复杂,破解私钥的难度将极高,从而保证信息安全。
02 为什么RSA难以被破解?
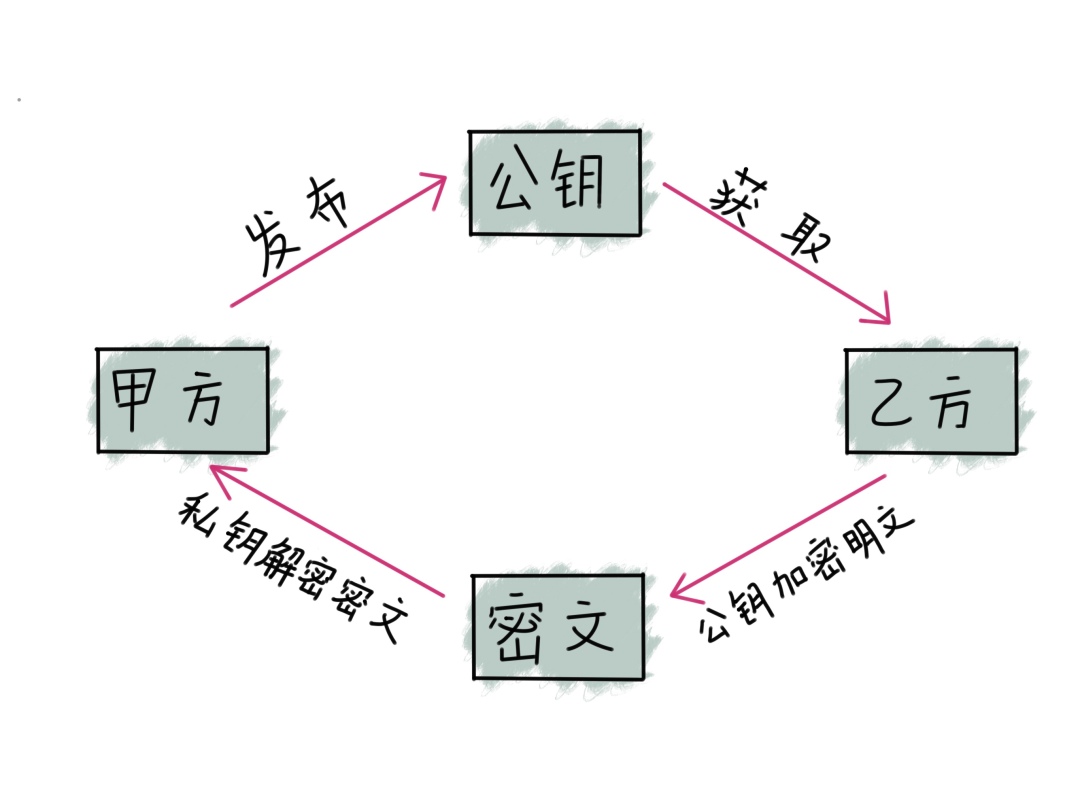
△ RSA原理
RSA算法基于一个十分简单的数论事实:将两个大质数相乘十分容易,但是想要对其乘积进行因式分解却极其困难,因此我们将两个大质数的乘积公开作为加密密钥。
RSA算法的核心是大整数N的因式分解问题。具体来说,给定N=p×q(p和q 是两个大质数),破解RSA需要从N中找到p和q,这是一个经典计算在有效时间内难以完成的任务。
例如,2048位的RSA密钥对应的N通常包含超过600位的十进制数字,分解这样的大整数在现有的经典计算能力下短时间内是不可能完成的。
现在,在中电信“天衍”量子计算云平台上,您可以免费体验加密和解密的过程。让我们一起踏上这个新奇的旅程,探索量子技术的奥秘吧!
平台地址:https://qc.zdxlz.com/

△ 体验入口
03 RSA加密流程
RSA的加密与解密流程包括以下几个步骤:
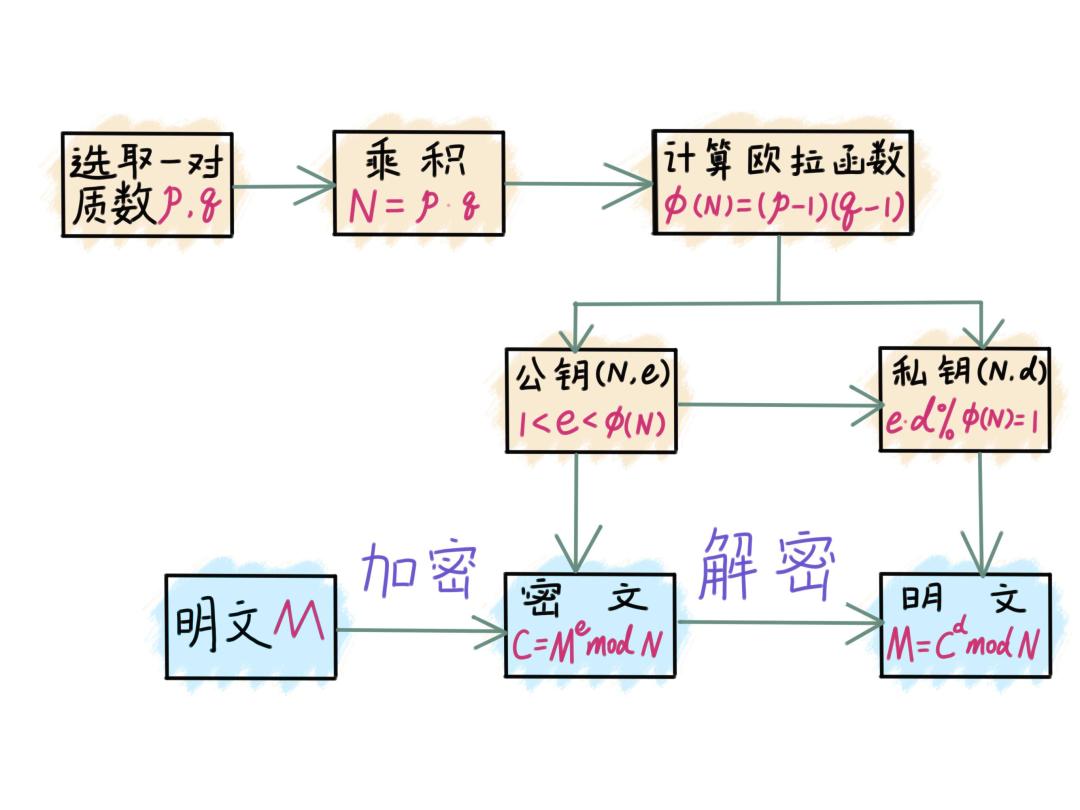
△ RSA流程
0 1 随机选取一对大数质数p和q
质数是指仅能被1和自身整除的正整数。选取的p和q越大,加密越安全。
0 2 计算模数N
N=p×q
例如,若p=97,q=89,则N=8633。将8699转换为二进制为10000111111011(14位),位数越长,加密越难破解。
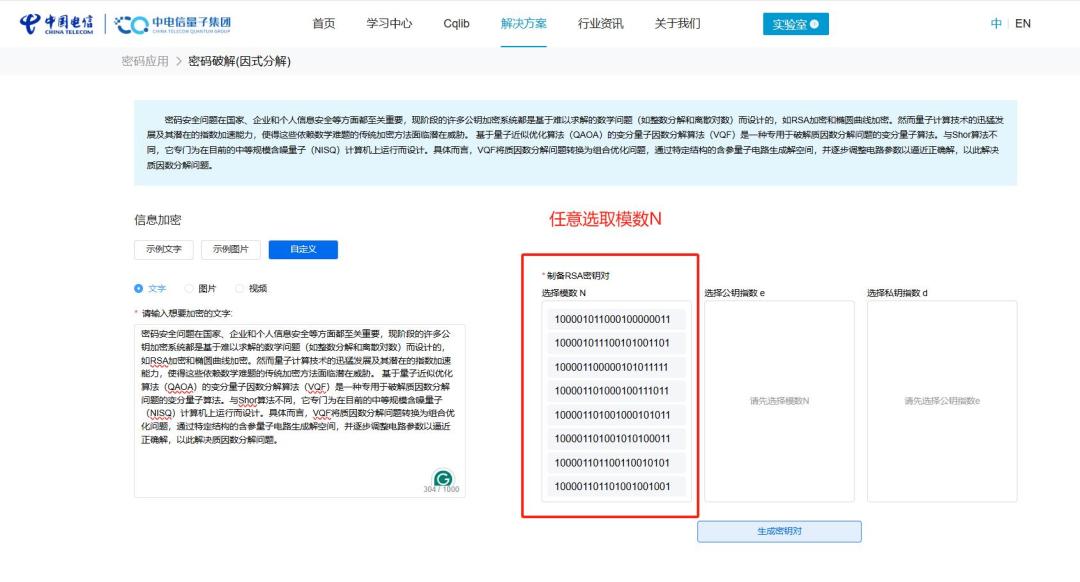
△ 选取模数N
0 3 计算欧拉函数
Φ(N)=(p-1)(q-1)
欧拉函数表示小于N且与N互质(整数的公因数只有1)的正整数个数。例如,当N=8时,互质数为 1、3、5、7(其中2、4、6都和8有公约数2),因此Φ(8)=4。
0 4 生成公钥e,N
1eΦ(N)
e是个在不等式范围里的随机数,且与Φ(N)互质。
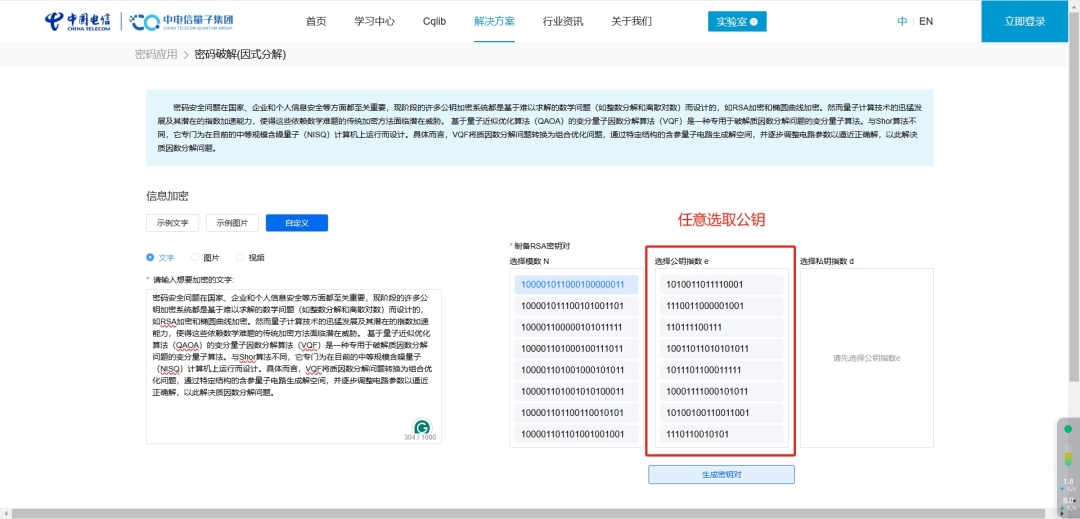
△ 选取公钥e,N
0 5 生成公钥d,N
其中d满足以下条件:
•e×d modΦ(N)=1
这里d可通过扩展欧几里得算法求解。
(扩展欧几里得算法:扩展欧几里得算法是求解二元一次方程(如ax+by=1)的有效方法,通过逐步递归计算最大公约数,推导出d)
•1dΦ(N)
•d与Φ互质

△ 私钥选取
0 6 公钥加密
加密公式:C=Memod N
其中M是明文,C是密文。mod表示取模运算,即计算余数。比如说9 mod 2=1。
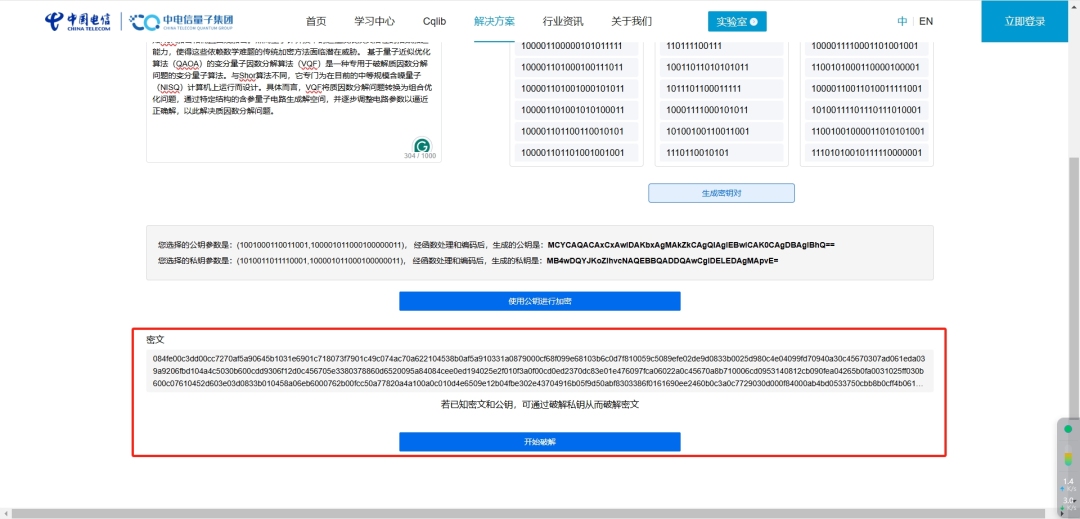
△ 生成密文
04 VQF算法概述
VQF是一种量子-经典混合算法,旨在通过量子计算的独特优势(如超高维态叠加)来优化特定目标函数。
该算法的核心思想是:在量子线路中利用参数化量子态表示优化问题的解空间,将问题转化为寻找最佳参数的一种迭代过程。这种方法结合了量子计算的强大计算能力和经典计算的优化能力,以期突破经典方法的瓶颈。
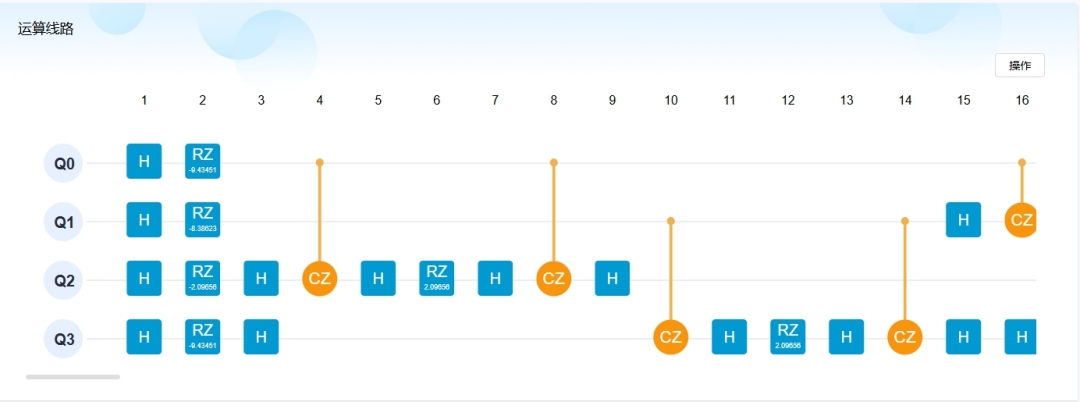
△ 完整运算线路请登录天衍量子计算云平台查看
05 VQF算法的核心步骤
0 1 数学预处理:简化方程
VQF算法的第一步是将因式分解问题N=p*q反过来,变为乘法问题p*q=N;再根据乘法表,将乘法问题转化为方程问题;最后根据各比特位的布尔关系对方程进行简化,减少变量(比特)数。
举个例子:分解143=1000 1111(8位数二进制)
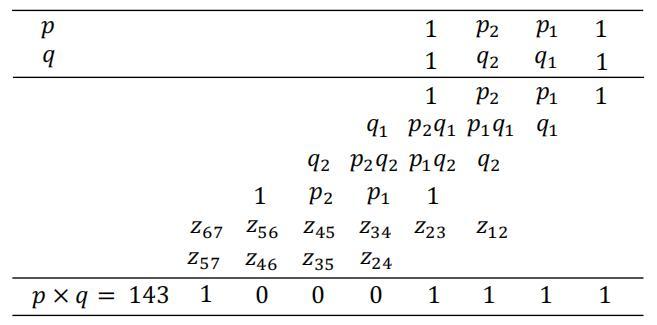
这里就会转化成一个解方程的问题:
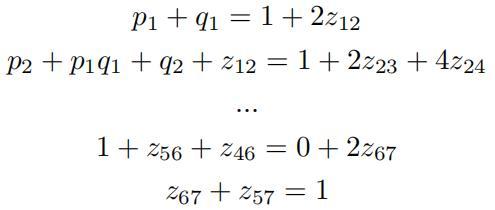
我们通过对方程的进一步简化,达到减少未知项的目的,从而更方便我们得到结果:
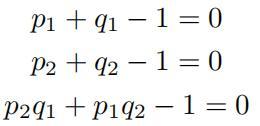
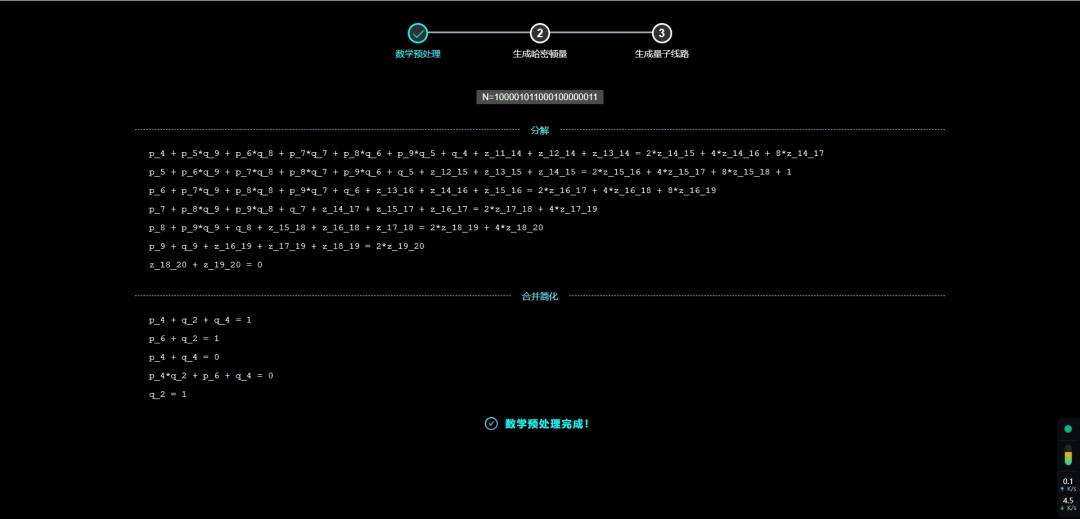
△ 天衍平台上体验过程截图-数学预处理
0 2 组合优化
在预处理完成后,将方程求解问题转化为组合优化问题。
利用代价函数来优化参数:
Cost=(p1+q1-1)2+(p2+q2-1)2+(p2q1+p1q2-1)2
将其中的参数调整成p1→x0;p2→x1;q1→x2;q2→x3。
由此可得:Cost=(x0+x2-1)2+(x1+x3-1)2+(x1x2+x0x3-1)2
0 3 量子问题转化
接下来,需要在量子计算机上将问题的核心计算量子化,通过
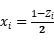
,将组合优化问题转化成适合量子计算机处理的哈密顿量问题。
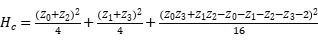
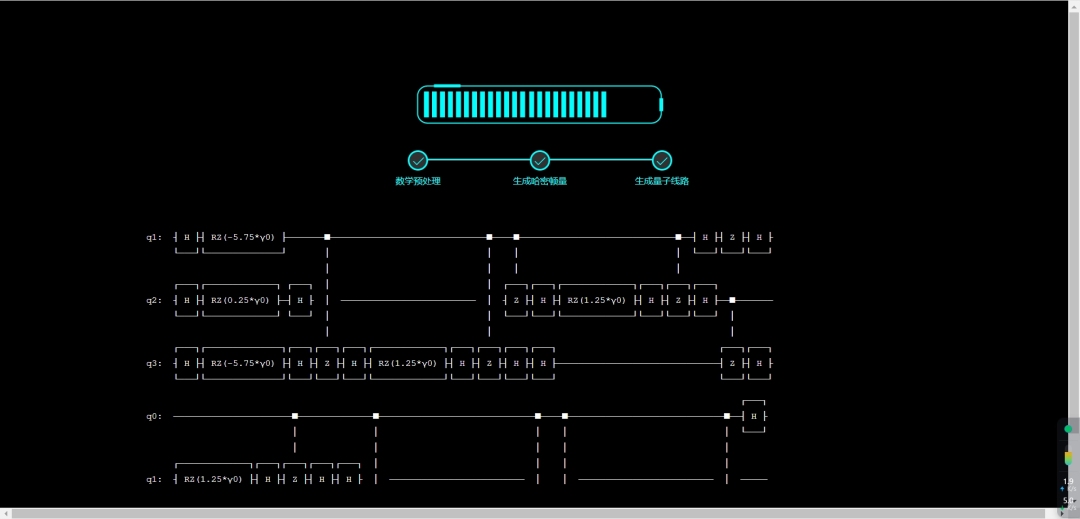
△ 线路图
0 4 多次迭代:参数优化与经典计算结合
VQF算法的精髓在于经典优化器和量子计算机的协同工作,通过多次迭代,逐步逼近问题的最优解,同时避免陷入局部极小值。
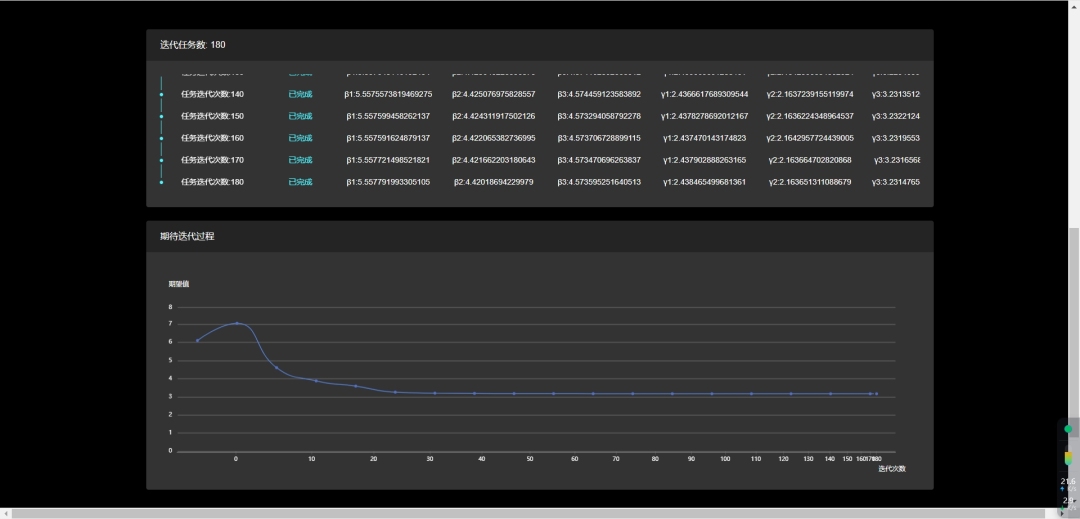
△ 多次迭代
0 5 破译结果
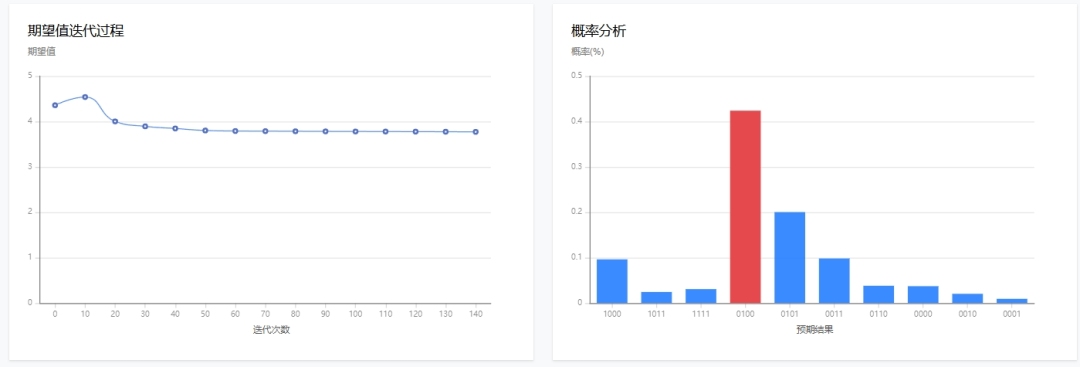
△ 破译结果
结果图中,期望值随着迭代次数逐渐趋于平静,说明算法在优化过程中逐步收敛,找到了可能的最优解或接近最优解的参数设置。而柱状图中红色标记的柱子对应的概率显著高于其他量子态,表明算法成功将量子态的概率分布集中在最优解上。
结语
变分量子分解算法(VQF)利用量子叠加和并行计算特性加速因子搜索,通过结合经典优化,显著降低了对量子比特数量和门深度的需求。不仅展示了量子算法在整数分解中的计算潜力,还表明即使在硬件受限的情况下,量子计算在该领域依然具有实际可行性,为未来分解更大整数提供了技术可能性。
想要了解更多量子知识
就来“天衍”量子计算云平台!

扫码或复制链接至PC端访问 https://qc.zdxlz.com/